The troubles are far from over, this time it’s the docking program on the ferry that’s not compatible with the port computer system. We need to emulate the port’s software by using a bitmasking system to figure out the correct instructions. Let’s see if we are able to implement this logic with Power BI.
If you want to follow along please download AdventOfCode2020.pbit and check Day 1 post for instructions.
Part 1
As usual there’s a file with a set of instructions. Some lines refer to memory addresses and others to bitmasks. We need to apply the mask to the values stored in the memory addresses beneath it until we reach the next mask repeating the process to the end of the file.
Applying bitmasks to bits is similar to groups operations on sets. You can read more on this Wikipedia link how it’s used. One of the more interesting applications is the linear solution to the Tower of Hanoi problem by using bitwise operations.
Let’s start by doing some basic transformations on our file:
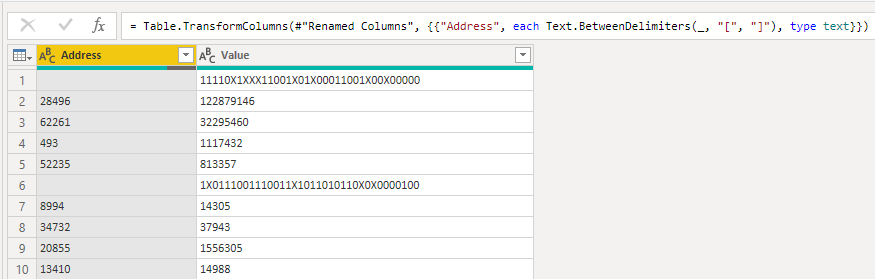
The next step is to create a positive mask and a negative one, to answer to the tricky part of forcing the “0”. By applying first the Or mask and then the And one we get to the result in the example:
# Initial values
mask = XXXXXXXXXXXXXXXXXXXXXXXXXXXXX1XXXX0X
orMask = 000000000000000000000000000001000000
andMask = 111111111111111111111111111111111101
# Applying first the orMask
value = 000000000000000000000000000000001011 (decimal 11)
orMask = 000000000000000000000000000001000000
result = 000000000000000000000000000001001011 (decimal 75)
# Then the andMask
value = 000000000000000000000000000001001011 (decimal 75)
andMask = 111111111111111111111111111111111101
result = 000000000000000000000000000001001001 (decimal 73)
Power Query already has functions to deal with bitwise operations.
What it doesn’t have is a binary type we can use. To deal with this
the easiest thing to do is to convert the masks to decimal by using a
function:
(mask as text, maskType as text) => let m = List.Reverse(Text.ToList(mask)) in List.Accumulate( {0..35}, 0, (seed, current) => if m{current} = maskType then seed + Number.Power(2,current) else seed )
With that we get this table:
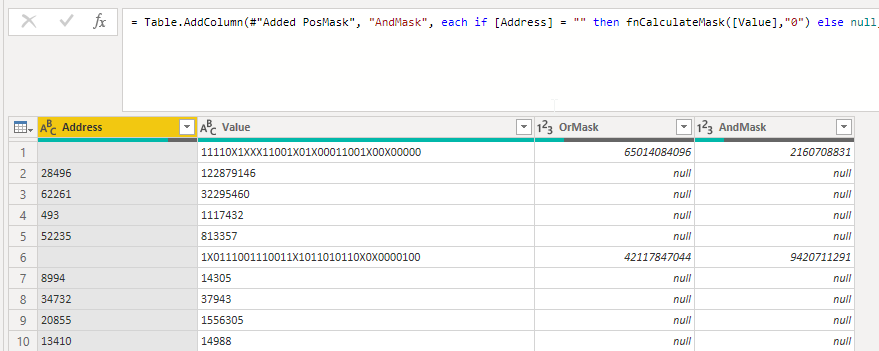
Filling down the values, applying the masks and removing the unnecessary lines:
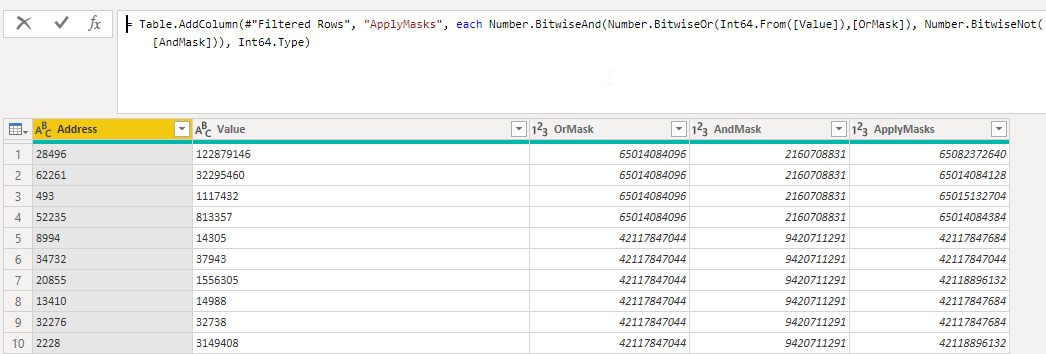
Removing the auxiliary columns and adding an index:
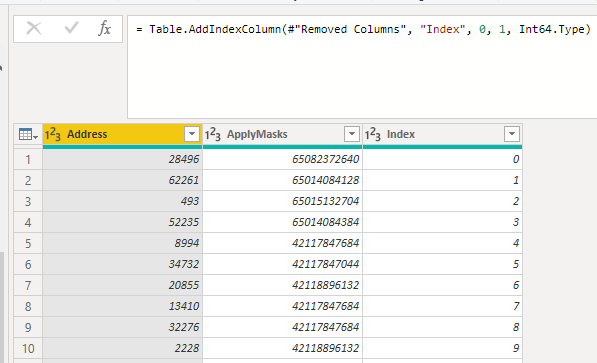
We added an index to help us with the last step because we must only consider the latest value that was written to an address. Taking advantage of the index we add a virtual column to the original table with the maximum value of index per address. Then is just a straight sum over the filtered table where the index of the address matches it maximum address.
Day 14 - Part 1 = CALCULATE(SUM('Day 14'[ApplyMasks]), FILTER( ADDCOLUMNS( 'Day 14', "MaxIndex", CALCULATE( MAX('Day 14'[Index]), ALLEXCEPT('Day 14', 'Day 14'[Address]) ) ), [Index] = [MaxIndex] ) )
Part 2
Now things are getting interesting. We have a kind of floating bit
that can make us write to several addresses simultaneously. It seems
that the challenge here is to be able to generate from a mask all the
possible combinations that are hiding in those special X bits.
Following the example provided in the puzzle page we can see that the
mask will be applied to the binary representation of the address value
and the X will be used in the operation. This prevents us from using
the native functions we have used before. So the first step is to
create a function that converts from decimal to 36-bit binary
representation. Nothing fancy where, just using the standard
mathematical algorithm and stuffing some zeros in the end:
fnDecToBin = (x as number) as text => let bin = List.Generate( () => x, each _ > 0, each Number.IntegerDivide(_,2), each Number.ToText(Number.Mod(_,2)) ), str = List.Accumulate( List.Reverse(bin), "", (s,c) => Text.Combine({s,c})), ret = Text.Combine({ Text.Repeat("0", 36-Text.Length(str)), str}) in ret
And then to create another function to apply the mask to the address:
fnApplyMaskX = (addressMask as text, xMask as text) as text => let am = Text.ToList(addressMask), xm = Text.ToList(xMask), ret = List.Transform( {0..35}, each if xm{_} <> "0" then xm{_} else am{_} ) in List.Accumulate( ret, "", (s,c) => Text.Combine({s,c}) )
Now the main course, we need to take a mask and generate all the
addresses where the values are to be written. The main algorithm idea
here is that we will create a table with just one column and we will
recursively join it with another table with two rows, a one and a zero
for each X in the mask. We start by splitting
“000000000000000000000000000000X1101X” on every X:
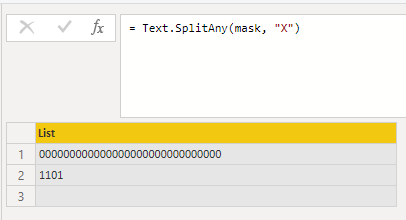
We take the head of that list as the beginning case and continue like this:
# Iteration 1
| Column1 |
| 000000000000000000000000000000 |
# Doing a Table.Combine
| Column1 |
| 0000000000000000000000000000000 |
| 0000000000000000000000000000001 |
# Iteration 2 we add the next block from
# the splitted list
| Column1 |
| 00000000000000000000000000000001101 |
| 00000000000000000000000000000011101 |
# Second Table.Combine
| Column1 |
| 000000000000000000000000000000011010 |
| 000000000000000000000000000000111010 |
| 000000000000000000000000000000011011 |
| 000000000000000000000000000000111011 |
After we get this last step we convert the binary to decimal and we have our addresses.
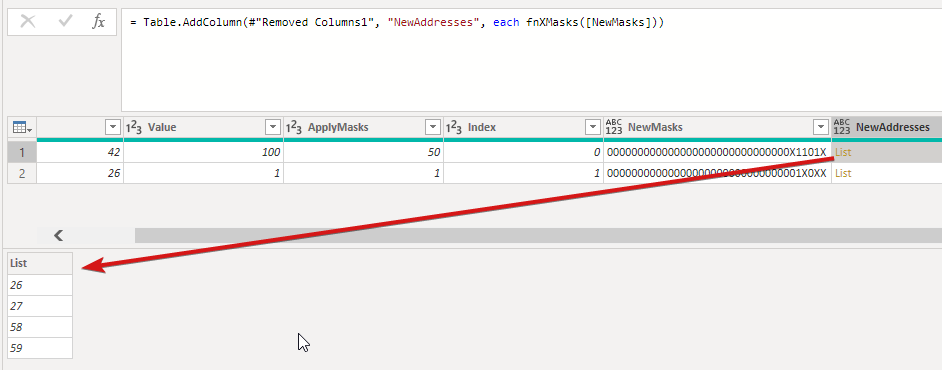
Now we expand the list of addresses to new rows and follow the same procedure as in part 1 by adding another index:
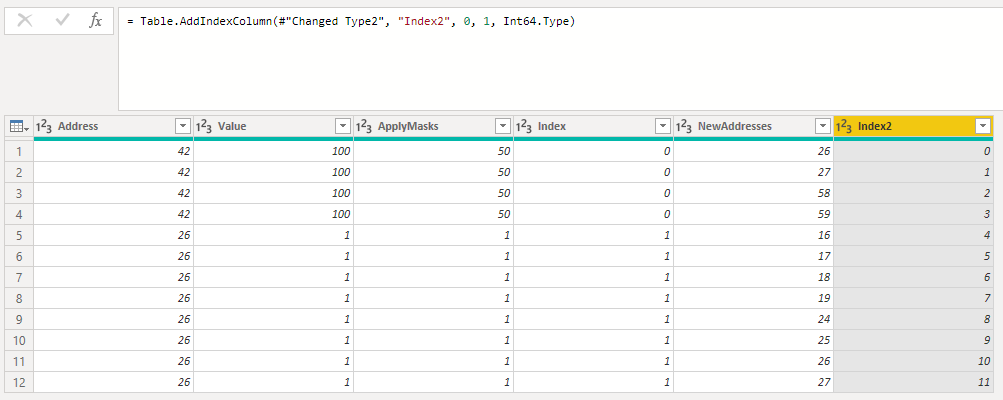
Now that the structure of the table was altered we have duplicate rows and we need to change the measure of part 1 to this:
Day 14 - Part 1 = SUMX( FILTER( SUMMARIZE( 'Day 14', 'Day 14'[ApplyMasks], 'Day 14'[Index], 'Day 14'[Address], "MaxIndex", CALCULATE( MAX('Day 14'[Index]), ALLEXCEPT('Day 14', 'Day 14'[Address]) ) ), [Index] = [MaxIndex]), [ApplyMasks] )
The logic is essentially the same, we just use SUMMARIZE to remove
the duplicate rows instead of ADDCOLUMNS.
The measure for part 2 is almost identical as the old one we have made in part 1:
'Day 14'[Day 14 - Part 2] = SUMX( FILTER( ADDCOLUMNS( 'Day 14', "MaxIndex", CALCULATE( MAX('Day 14'[Index2]), ALLEXCEPT('Day 14', 'Day 14'[NewAddresses]) ) ), [Index2] = [MaxIndex]), [Value] )
Conclusion
An interesting problem that reused some ideas from other puzzles we solved in this series. And now it’s time to think about the next one. See you soon.
Have fun!!
