Advent of Code 2020 - Day 5

Power BI / DAX / Power Query / Advent of Code 2020

This problem seems a lot of work at first but in reality it’s just binary number conversion to decimal.

Picking up the provided example:

FBFBBFF RLR

If we replace the lower half [F, L] by 0, and the upper half [B, R] by 1 we get:

0101100 101

Doing the conversions:

\begin{equation} \begin{aligned} (0101100)_2 &= 0*2^6 + 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 0*2^0 \\\ &= 32 + 8 + 4 \\\ &= 44 \\\ \\\ (101)_2 &= 1*2^2 + 0*2^1 + 1*2^0 \\\ &= 4 + 1 \\\ &= 5 \end{aligned} \end{equation}

So let’s try to implement the same idea using Power Query.

If you want to follow along please download AdventOfCode2020.pbit and check Day 1 post for instructions.

Part 1

After we load the file and do some splitting

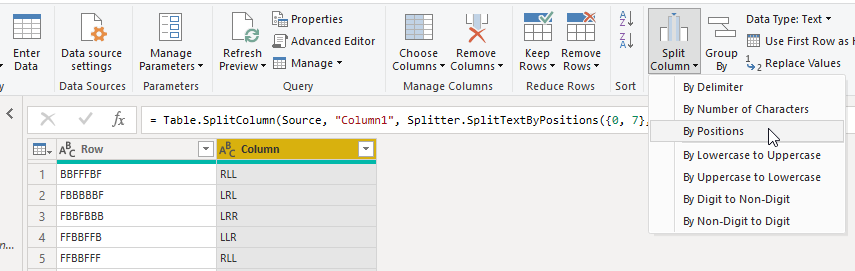
And then some replacing:

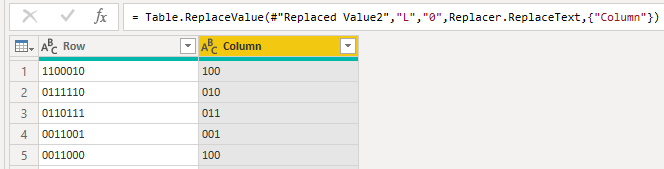
Figure 1: Replacing the letters with the numbers

Figure 1: Replacing the letters with the numbers

We are ready to aplly this custom function that does the the math for us:

(input as text) as number =>
let
    numberList = Text.ToList(input),
    len = List.Count(numberList)-1,
    Result = List.Sum(
                List.Transform(
                    {0..len}
                    , each Number.FromText(numberList{_}) * Number.Power(2, len - _)
                )
            )
in
    Result

We are using the not so common function List.Transform. What this function does is to return a new list from the results of applying a function to the elements of the list passed as a parameter. In essence it works like a map function.

Starting from a list that goes from 0 till the length of the input minus 1, in each step we are going to get the number in that array position and multiply its value by 2 to power of the length minus the current position. Just like in the mathematical definition.

Here’s an example in pseudo-power-query-code that should clear any doubts:

numberList = {"1", "0", "1"}

List.Transform(
    {0,1,2}
    Number.FromText(number{_}) * Number.Power(2, 2 - _)
)

=>

{
    Number.FromText(number{0}) * Number.Power(2, 2 - 0),
    Number.FromText(number{1}) * Number.Power(2, 2 - 1),
    Number.FromText(number{2}) * Number.Power(2, 2 - 2)
}

=>

{
   1 * 2^2,
   0 * 2^1,
   1 * 2^0
}

=>

{4, 0, 1}

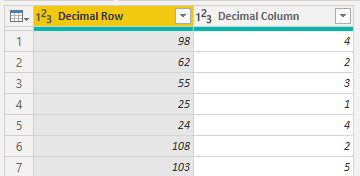
Invoking the function for each of the columns should lead to something like this:

Finishing this part with some DAX to get the highest seat id:

MAXX('Day 5', 8 * 'Day 5'[Decimal Row] + 'Day 5'[Decimal Column])

Part 2

Now we need to find our seat id in the data table.

The easiest solution that came to my mind was to use the EXCEPT(<LeftTable>, <RightTable>) DAX function. This will gives all the rows in the left table that do not exist in the right table.

If we are able to generate all the possible ids as the LeftTable, doing the except should give us the missing value:

//Adding the column with the boarding ids
VAR _boardingIds =
    ADDCOLUMNS (
        'Day 5',
        "BoardingIds",
            8 * 'Day 5'[Decimal Row] + 'Day 5'[Decimal Column]
    )
VAR _minID = MINX ( _boardingIds, [BoardingIds] ) //calculate the minimum id
VAR _maxID = [Day 5 - Part 1]                     //get the maximum id
VAR _allIDs = GENERATESERIES ( _minID, _maxID )   //all the values between min and max
RETURN
    EXCEPT (
        _allIDS,
        SELECTCOLUMNS ( _boardingIds, "Boarding IDs", [BoardingIds] )
    )

Conclusion

This puzzle was a nice show case for the List.Transform function. It allow us to do some things in Power Query that would be difficult to implement or very slow to do otherwise. In the next posts on Advent of Code we are going to explore some of the other friends of List.Transform that extend greatly the normal usage of the language.

Have fun!!

 Share!