Advent of Code 2020 - Day 7

Power BI / DAX / Power Query / Advent of Code 2020

Day 7: Handy Haversacks is the hardest puzzle to solve using only Power BI until now. It took me a lot of time to find a viable and fast solution.

I have first tried to solve this using DAX PATH but had issues with the different levels of recursion. It was possible in the real data input for the same bag to be child of different bags in different levels. Only after a deep dive on using the List.Generate a light began to appear on the end of the tunnel.

Here are some of the great references that helped me:

You will also see some references on the code to List.Buffer and Table.Buffer. They are very similar functions that load the object to memory and prevent it from being reevaluated. Without them Power Query will keep trying to reload the text file from disk slowing to a halt our execution times. See this post from Chris Webb for more information:

If you want to follow along please download AdventOfCode2020.pbit and check Day 1 post for instructions.

Data preparation

The first part asks us to find how many bag colors can eventually contain at least one shiny gold bag.

This is our initial data:

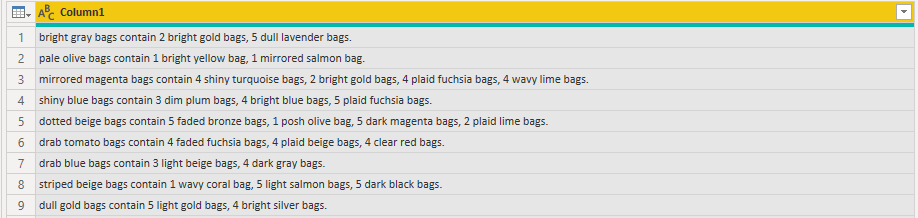
And with the usal find and replace we get to:

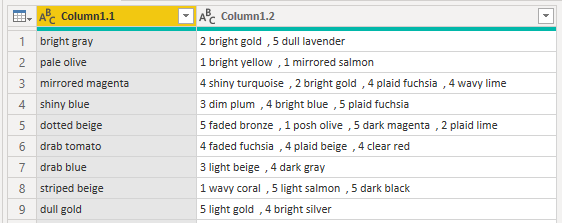
Now we use the advanced section of ‘Split column by delimeter’ to create a new row for each comma found:

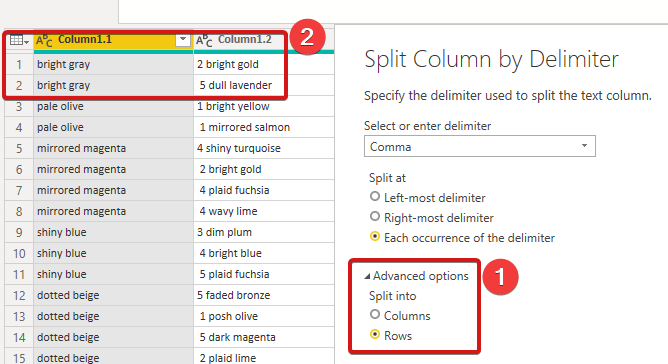
And finish the the data preparation creating a new column with the quantities:

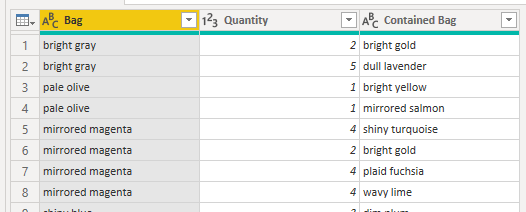
Part 1

My idea to solve this puzzle is to create some kind of self joining loop. Starting from all the bags that can contain directly a shiny gold bag and keep joining that input with their parent bags until it’s impossible to continue joining.

The first parameter in our List.Generate is the initial condition. In our case we start from the direct ascendants of the shiny gold bags.

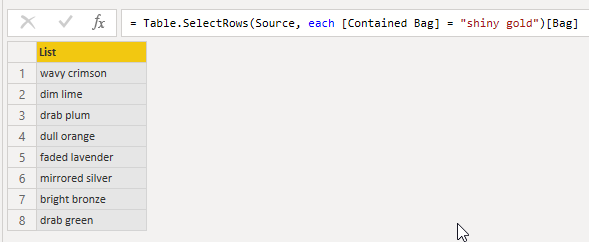
The second parameter is the stop condition. In this case we will stop when there’s no more ascendants. The third parameter is the iteration step:

listAcc =
        List.Generate(
            () => [Current=listThatContainShinyGoldDirectly],
            each not List.IsEmpty([Current]),
            (f) =>
                [Current =
                    List.Buffer(
                        List.Distinct(
                            Table.SelectRows(Source,
                                each List.Contains(f[Current], [Contained Bag]))[Bag]))]
        )

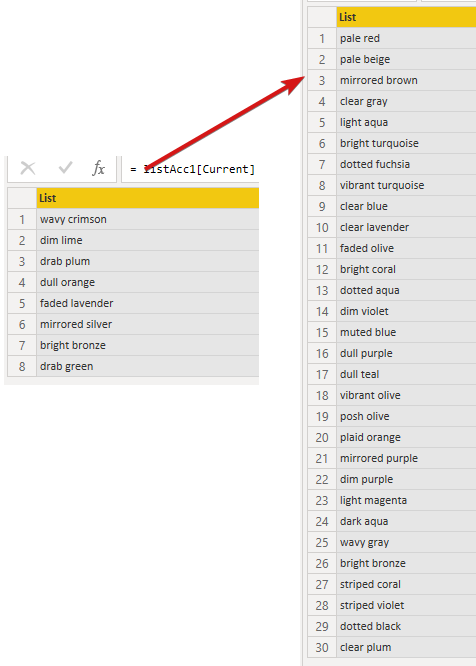
In each iteration step we assign to the value of Current the ascendants of the previous Current value. Here’s the first two steps to give an idea of what’s going on:

In the end we get this table:

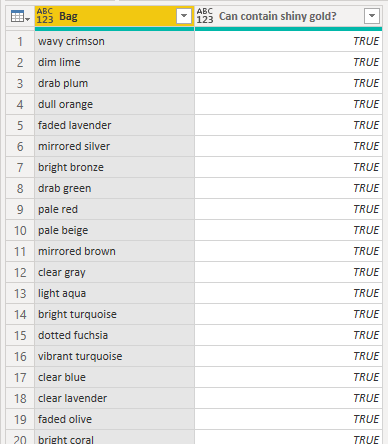
The only thing left is to left merge this auxiliar table with the 'Day 7' and count all those TRUE values.

Day 7 - Part 1 =
CALCULATE(
    COUNTROWS('Day 7'),
    'Day 7'[Can contain shiny gold?] = TRUE())

Part 2

Now for the tricky part. We need to calculate the number of bags that our shiny gold bag can contain. For this we are going to use a similar strategy as in Part 1 with a catch, we need to pass along to the next step the number of current bags.

Because of this passing along we now need a more complicated join. To obtain this we can use a function like this:

makeJoin =
        (t as table) as table =>
            let
                s1 = Table.NestedJoin(t, {"Contained Bag"}, buffer, {"Bag"}, "buffer", JoinKind.Inner),
                s2 = Table.ExpandTableColumn(s1, "buffer",
                                              {"Bag", "Quantity", "Contained Bag"},
                                              {"Bag.1", "Quantity.1", "Contained Bag.1"}),
                s3 = Table.AddColumn(s2, "Qty", each [Quantity]*[Quantity.1]),
                s4 = Table.RemoveColumns(s3,{"Bag", "Quantity", "Contained Bag", "Quantity.1"}),
                s5 = Table.RenameColumns(s4, {{"Bag.1", "Bag"},
                                              {"Qty", "Quantity"},
                                              {"Contained Bag.1", "Contained Bag"}})
            in
                s5

We take out current step, join with the master table to get the lines where our contained bags contain others bags. Then we multiply the quantities and rename the columns so that our contained bags become the bags so that we can use this new table as the next iteration step.

Figure 1: Current step

Figure 1: Current step

Figure 2: Joining and multiplying

Figure 2: Joining and multiplying

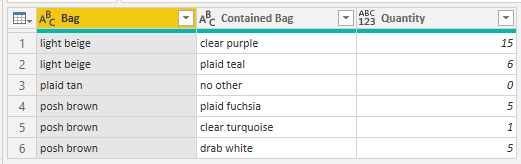
Figure 3: Ready for the next iteration

Figure 3: Ready for the next iteration

Now that we know how to iterate each step, we need to create the loop:

List.Generate(
            ()=> [Step=x1, Acc=0],
            each Table.RowCount([Step]) > 0,
            each [
                Step = makeJoin([Step]),
                Acc = List.Sum([Step][Quantity])
            ]
            , each [Acc]
        )

Our initial value will be a record containing the table on Figure 1 and an Acc to keep the total bags on each level. The second parameter validates if we can continue, stopping when we have no more rows returned after joining. The third parameter assigns to Step the result of the join and to Acc the sum of bags. Finally we return the list with the total of bags for each step.

Summing this list will give us the solution for the puzzle.

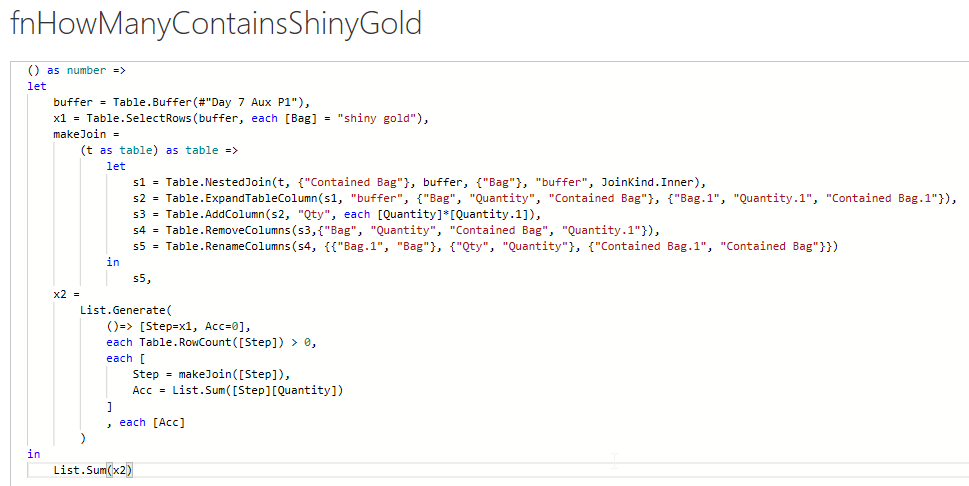
Figure 4: Final code

Figure 4: Final code

Conclusion

This puzzle was a great learning experience. I loved how elegant and efficient is the found solution for this naturally recursive problem. A great showcase for the List.Generate that I’m sure will be a great tool to solve future problems.

Have fun!!

 Share!